Normalenform einer Ebene
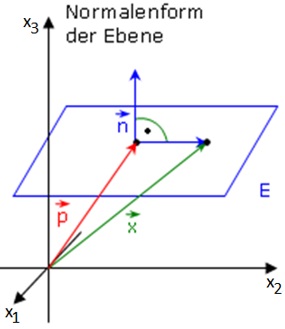
Eine besonders einfache Darstellung einer Ebene ergibt sich mit Hilfe eines Normalenvektors,
also eines Vektors der senkrecht zur Ebene steht. Dazu gehen wir wieder von eine festen
Punkt P (durch den Stützvektor repräsentiert) auf der Ebene aus und einem beliebigen Punkt X
in der Ebene. Da der Verbindungsvektor
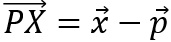senkrecht zum Normalenvektor steht,
ist das Skalarprodukt Null.
Daraus erhält man die Normalenform:
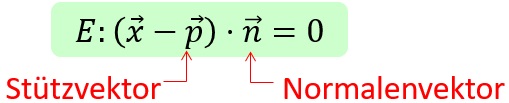
Beispiel:
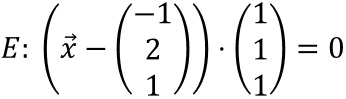
Koordinatenform der Ebene
Durch Ausmultiplizieren der Normalenform erhält man die Koordinatenform:
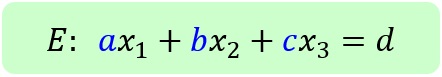
Beispiel: E: 2x1-3x2+1x3=4
Der Normelenvektor von E ist dann
.
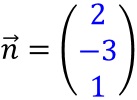Aufgabe
Gegeben sei die Ebene E durch
.
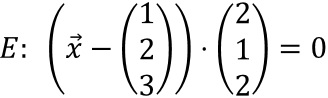- Ermitteln Sie eine Koordinatengleichung von E.
- Liegt der Punkt P(7|0|-3) auf E?
Lösung a.
Die Lösung lässt sich auf verschiedene Arten bestimmen.
Methode 1
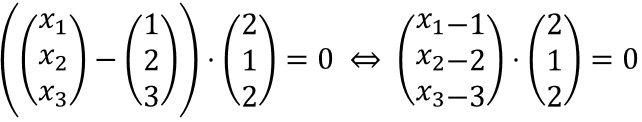
2x1-2+x2-2+2x3-6=0 ⇒
E: 2x1+x2+x3=10
Methode 2
Die Koordinaten des Normalenvektors sind die Koeffizienten in der Koordinatenform. Wir können daher sofort E: 2x1+x2+2x3=d mit noch unbekanntem d schreiben. Nun brauchen wir lediglich einen Punkt, der in der Ebene liegt und durch Einsetzen erhalten wir d. Der Stützvektor führt zu einem solchen Punkt. Durch Einsetzen erhalten wir 2·1+2+2·3=10=d. Somit gilt:
E: 2x1+x2+x3=10
Lösung b.
Setze einfach die Koordinaten von P ein (egal ob in die Koordinatenform oder in die Normalenform) und prüfe, ob die Koordinatengleichung erfüllt wird: 2·7+0+2·(-3)=8≠10
Ergebnis: Der Punkt P liegt nicht in E.
| Downloads |
PowerPoint